Spectral Theorem For Symmetric Matrices

Spectral Theorem

• Eigenvalues and eigenvectors of symmetric matrices

• The symmetric eigenvalue decomposition theorem

• Rayleigh quotients

Eigenvalues and eigenvectors of symmetric matrices

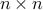Let be a square, symmetric matrix. A real scalar 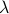is said to be an eigenvalue of if there exist a non-zero vector 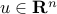such that

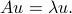
The vector is and then referred to as an eigenvector associated with the eigenvalue 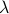. The eigenvector is said to be normalized if 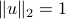. In this case, we have

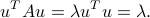
The estimation of is that it defines a management forth behaves but similar scalar multiplication. The amount of scaling is given by . (In High german, the root ''eigen'', means ''cocky'' or ''proper''). The eigenvalues of the matrix are characterized by the feature equation

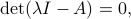
where the note 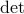refers to the determinant of its matrix argument. The function with values 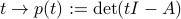is a polynomial of degree 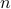chosen the characteristic polynomial.

From the key theorem of algebra, whatsoever polynomial of degree 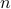has 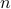(perchance not distinct) complex roots. For symmetric matrices, the eigenvalues are real, since 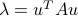when , and is normalized.

Spectral theorem

An important event of linear algebra, called the spectral theorem, or symmetric eigenvalue decomposition (SED) theorem, states that for whatsoever symmetric matrix, in that location are exactly 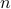(perchance not distinct) eigenvalues, and they are all real; further, that the associated eigenvectors can be called and then as to class an orthonormal basis. The result offers a unproblematic way to decompose the symmetric matrix as a product of simple transformations.

Theorem: Symmetric eigenvalue decomposition

Here is a proof. The SED provides a decomposition of the matrix in simple terms, namely dyads.

Nosotros check that in the SED above, the scalars 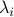are the eigenvalues, and 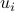'due south are associated eigenvectors, since

The eigenvalue decomposition of a symmetric matrix can be efficiently computed with standard software, in fourth dimension that grows proportionately to its dimension 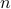as . Here is the matlab syntax, where the first line ensure that matlab knows that the matrix is exactly symmetric.

Matlab syntax

>> A = triu(A)+tril(A',-1); >> [U,D] = eig(A);            

Example:

• Eigenvalue decomposition of a 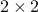symmetric matrix.

Rayleigh quotients

Given a symmetric matrix , we can limited the smallest and largest eigenvalues of , denoted and respectively, in the and so-called variational class

For a proof, see hither.

The term ''variational'' refers to the fact that the eigenvalues are given as optimal values of optimization problems, which were referred to in the past as variational problems. Variational representations be for all the eigenvalues, but are more complicated to state.

The interpretation of the above identities is that the largest and smallest eigenvalues is a measure of the range of the quadratic function 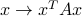over the unit Euclidean ball. The quantities above can be written as the minimum and maximum of the then-chosen Rayleigh caliber .

Historically, David Hilbert coined the term ''spectrum'' for the set of eigenvalues of a symmetric operator (roughly, a matrix of infinite dimensions). The fact that for symmetric matrices, every eigenvalue lies in the interval somewhat justifies the terminology.

Example: Largest singular value norm of a matrix.

Spectral Theorem For Symmetric Matrices,

Source: https://inst.eecs.berkeley.edu/~ee127/sp21/livebook/l_sym_sed.html

Posted by: crofootithoust.blogspot.com

Share this post